Persamaan Lingkaran
Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak sama terhadap suatu titik tertentu. Titik tertentu itu disebut pusat lingkaran, sedangkan jarak titik terhadap pusat lingkaran disebut jari-jari lingkaran.
Gambar dibawah ini menunjukkan lingkaran dengan pusat P dan jari-jari r.
A. Persamaan Lingkaran
1. Persamaan lingkaran yang berpusat O (0, 0) dan jari-jari r
Pada lingkaran disamping jari-jari atau r = OP, OQ = x dan PQ = y.
Jarak dari O (0, 0) ke P (x, y) adalah.
Berdasarkan rumus Pythagoras
Jadi persamaan lingkaran dengan pusat O (0, 0) dan jari-jari r adalah x2 + y2 = r2
Contoh :
Tentukan persamaan lingkaran yang berpusat O (0, 0) dan jari-jari 5
Jawab :
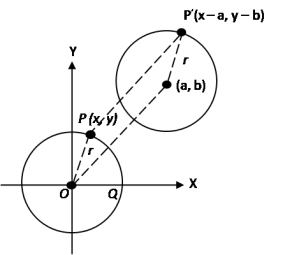
2. Persamaan lingkaran yang berpusat P (a, b) dan berjari-jari r
Persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r dapat diperoleh dari persamaan lingkaran yang berpusat di (0, 0) dan berjari-jari r dengan menggunakan teori pergeseran. Jika pusat (0, 0) bergeser (a, b) maka titik (x, y) bergeser ke (x + a, y + b).
Kita peroleh persamaan.
Persamaan lingkaran menjadi (x’– a)2 + (y’ – b)2 = r2
Jadi persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r adalah (x- a)2 + (y – b)2 = r2
Contoh 1 :
Tentukan persamaan lingkaran yang berpusat di (3, 2) dan berjari-jari 4
Jawab :
Pusat (3, 2) maka a = 3 dan b = 2
Persamaan lingkaran (x- a)2 + (y – b)2 = r2
(x- 3)2 + (y – 2)2 = 42
(x- 3)2 + (y – 2)2 = 16
Contoh 2 :
Tentukan persamaan lingkaran berpusat di titik P(2, 3) yang melalui Q(5, -1)
Jawab :
Pusat (2, 3) maka a = 2 dan b = 3
Persamaan lingkaran (x- a)2 + (y – b)2 = r2
(x- 2)2 + (y – 3)2 = 252
B. Bentuk umum persamaan lingkaran
Persamaan lingkaran yang berpusat P(a, b) dan berjari-jari r adalah
(x- a)2 + (y – b)2 = r2
x2 – 2ax + a2 + y2 – 2by + b2 = r2
x2+ y2 – 2ax – 2by + a2+ b2– r2 = 0 atau x2+ y2 + Ax + By + a2+ b2+ C= 0
Jadi bentuk umum persamaan lingkaran x2+ y2 + Ax + By + a2+ b2+ C= 0
Contoh :
Tentukan pusat dan jari-jari lingkaran x2+ y2 – 4x +2y – 20= 0
Jawab :
A = -4, B = 2, dan C = -20

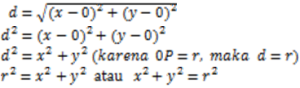
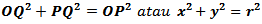
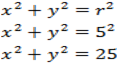
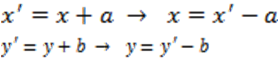
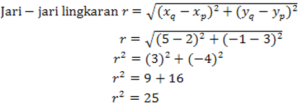
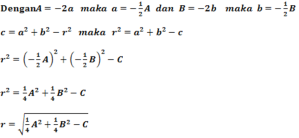

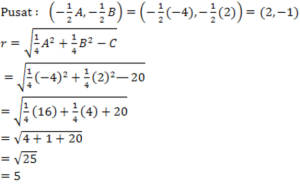



Absen: David adi firdaus
BalasHapusKelas : XI TKR OA
Absen: Alfian fahmi P
BalasHapusKelas : XI TKR OA
Absen ALDYAZ PRAMUDYA R
BalasHapusKelas:XI TKR OA
Nama:Ginar nurcahyo
BalasHapusAbsen:26
Kelas:XI TKR OA
Nama:indra wicaksono
BalasHapusAbsen:28
Kls:XI TKR OA
Absen:Bayu bagus Prasetya
BalasHapusNo:10
Kelas: XI TKR Oa
Absen:Bagas adi saputra
BalasHapusNo : 9
Kelas : XI TKR oA
absen: Farhan abriansyah
BalasHapusno : 21
kelas : XI TKR OA
Absen:Fhirza Yudha pratama
BalasHapusNo:20
Kelas: XI TKR OA